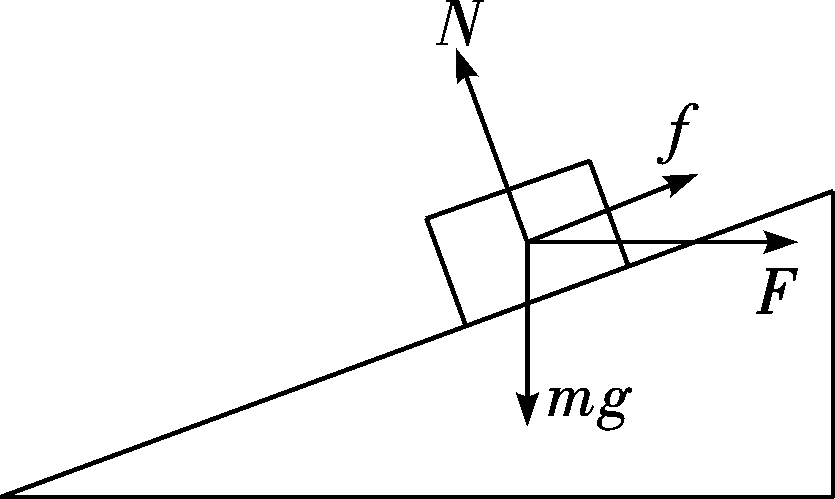
一口气吹起木块，到底是不是伯努利原理

这款玩具，你是否曾经尝试过？那些难以抓取的木质积木。玩法相当简便，只需将圆柱形的木块放入凹槽中，确保外围的方块保持静止，然后小心地将中间的圆形木块取出。

用手揪，揪，揪，扣，扣，扣，根本弄不出来，怎么办？

看看墙上这公式，流体力学里最经典的N-S方程。

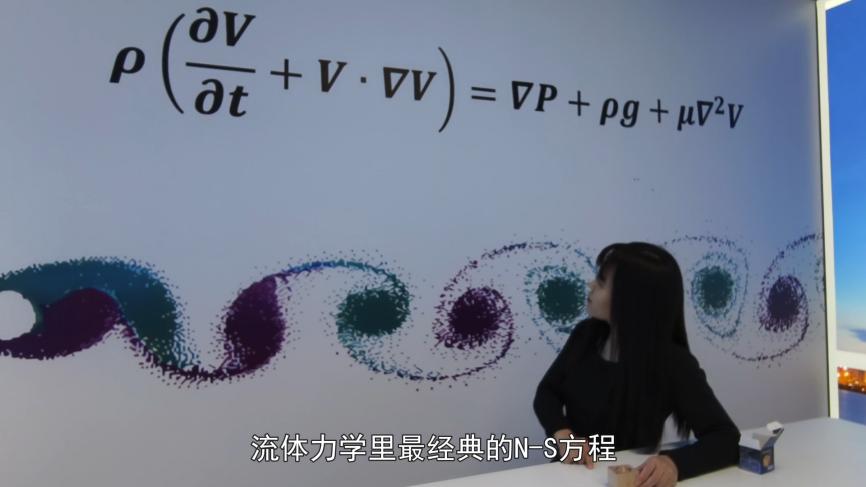
所以，一口气把木块吹出来。

这种方法并不罕见，众多博主曾展示过。那么，其背后的原理究竟是什么呢？

网络中普遍存在一种基于伯努利原理的解释：吹气使得圆柱顶部的气体流速增加，流速的提升导致压强降低，从而在上表面形成低压区，使得圆柱被吸起。然而，这种做法是对伯努利原理的一种典型误用。

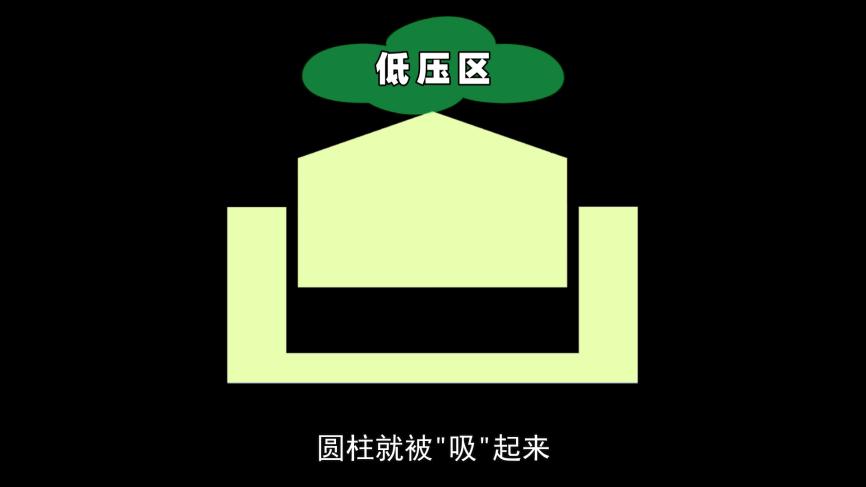
我们采用流体仿真软件AICFD进行一次基础模拟实验，以细管口模拟人嘴形态kaiyun.ccm开yun体育app官网网页登录入口，并设定吹气时的速度为20米每秒。

经过计算，我们发现圆柱的上表面所受的压力并未减小，反而超过了周围环境的压力。这一结果直接反驳了之前的说法。

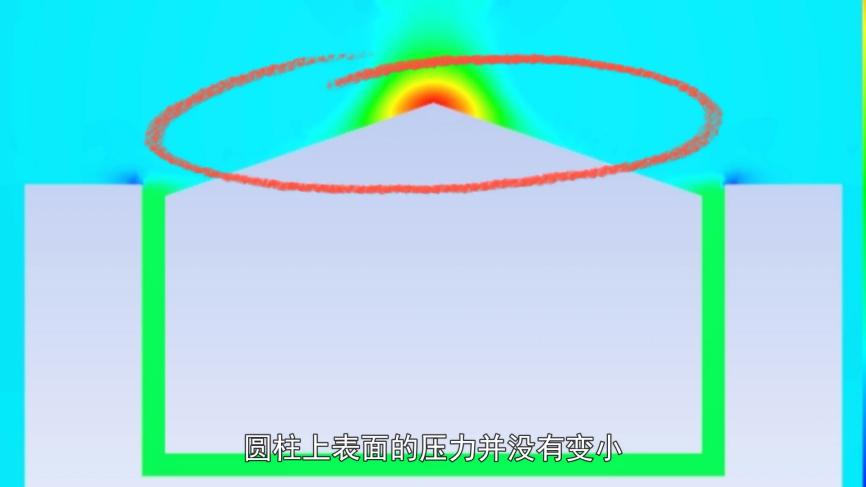
那么，真正的缘由或许非理工科背景的人更能通过直观感受领悟，简单来说，气流沿着斜坡向下流动，对缝隙中的空气施加压力，使得该处气体压力升高，从而将木块推起。

若稍作非通俗性的表述，那么便是：当运动中的流体遭遇阻力时，其部分动能压力将转化为静态压力。

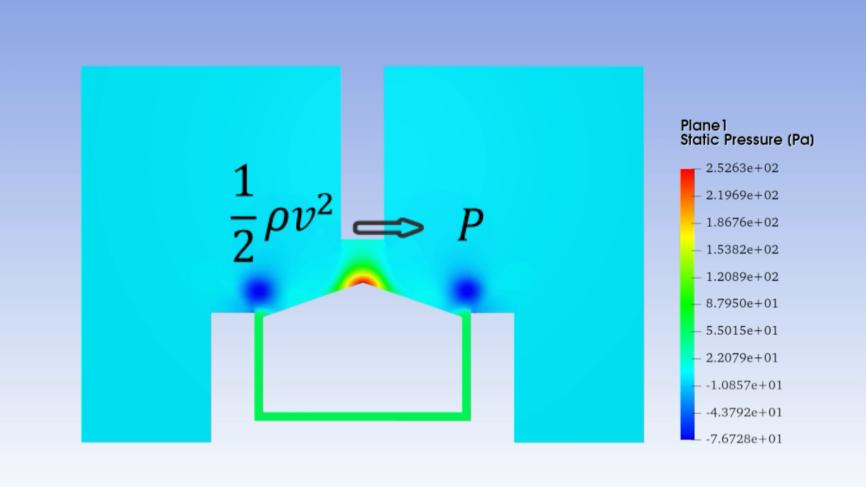
在此场景下，气流首次遭遇阻力出现在上方，因此上方形成了一个微小的区域，该区域气压较高，随后气流调整路径，沿着斜坡向低处流动。紧接着，气流在经过环形缝隙时再次遭遇阻力，随后它转向斜上方继续前行。

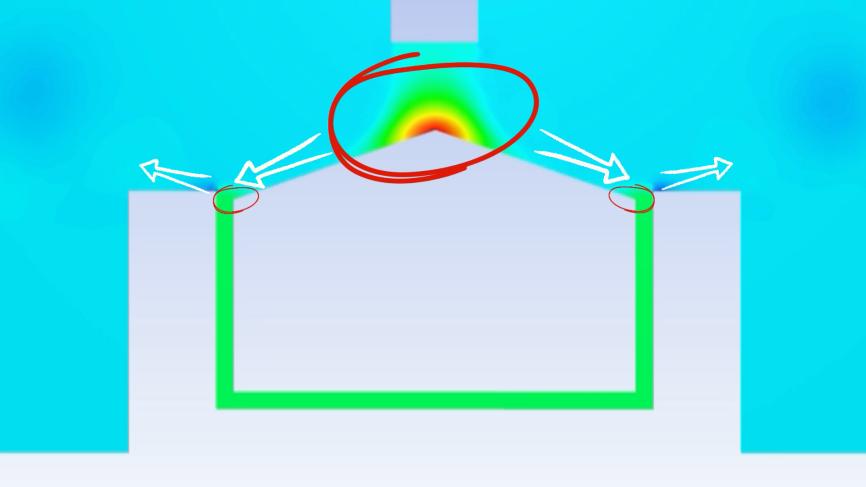
观察速度云图后，我们发现整个流程中，缝隙内的空气几乎处于静止状态。据此kaiyun全站网页版登录，我们可以设想在缝隙顶部存在一层无形屏障，气流在上方翻涌，当气体冲击这层屏障时，部分动能转化为静压，导致压力上升，而屏障下方则保持风平浪静。

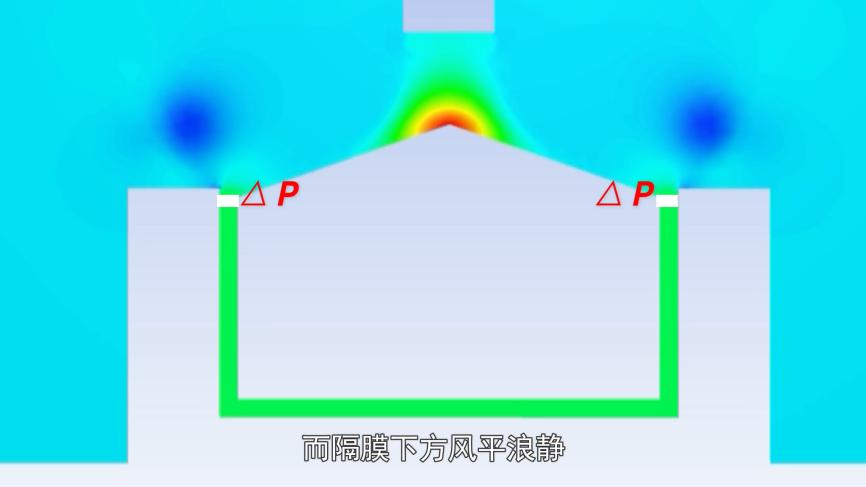
依据帕斯卡定律，在不可压缩且处于静止状态的流体中，当任一位置承受外部力的作用，导致压强增加时，这种压强增加会立即传递至流体的各个部分。

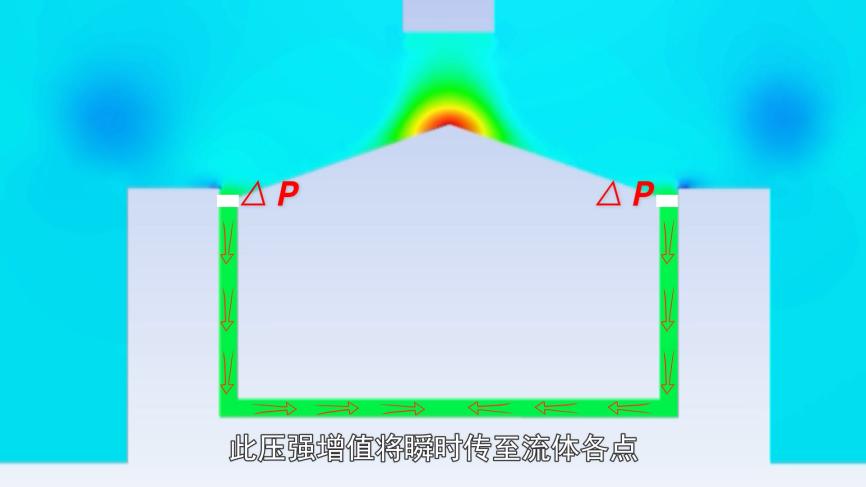
木块的底部全面承受着这种高压，一旦这种压力超过了上方小范围内施加的压力与木块自身重力的总和，木块便会随之升起。

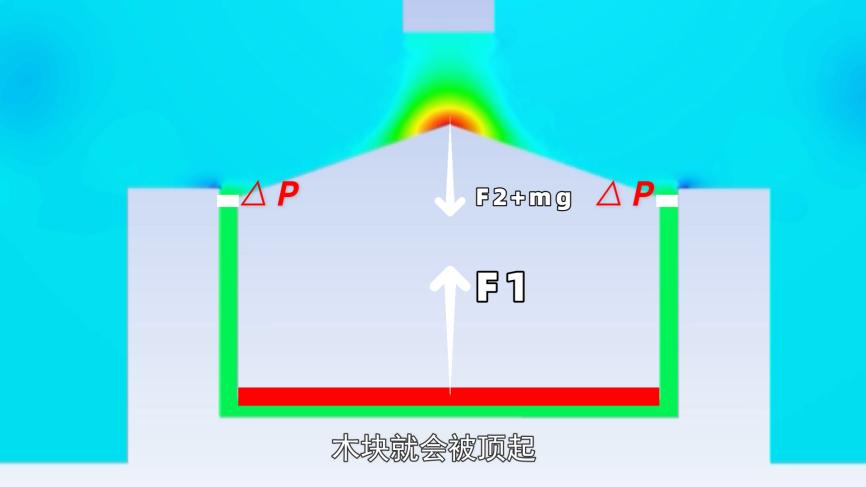
实际上，动压与静压之间的相互转化正是伯努利原理的核心所在，因此，我们可以说这一现象完全符合伯努利原理的解释。

并非流速增大导致上方压强减小；实际上，流速减小使得下方压强增大。

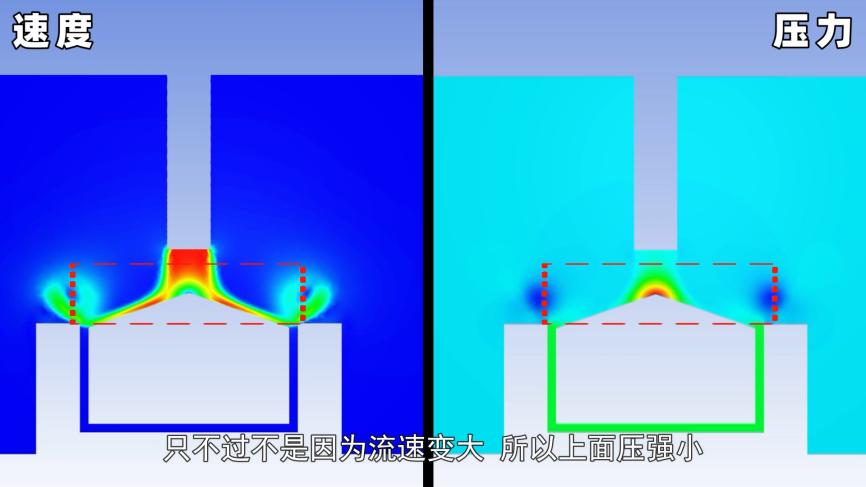
你提到上方空气流动速度较快，但为何压强并未降低，这主要是因为该速度是由你吹气，即你的肺部施加力量产生的，并非由静压变化所致，因此压强并未减小。今后若你观察到吹气造成空气流速增加，紧接着便断言由此导致压强降低的说法，几乎都是不准确的。

比如这么解释吹乒乓球的、吹纸的、吹袋子的、甚至吹沙子的。

重新审视这个木块的设计，其中一点尤为巧妙，那就是圆木块中间略微凹陷。这一设计显然有它的道理，因为如果木块表面平坦，我们就可以直接用手取走，那么这个拼图游戏也就失去了它的趣味性。

另一方面，若非凹陷，气流将沿着斜面两侧径直逸散，这将显著降低流动气体对缝隙的冲击力，导致动压转化为静压的过程减弱，进而使得底部的压力降低，木块因此也就不易被吹出。

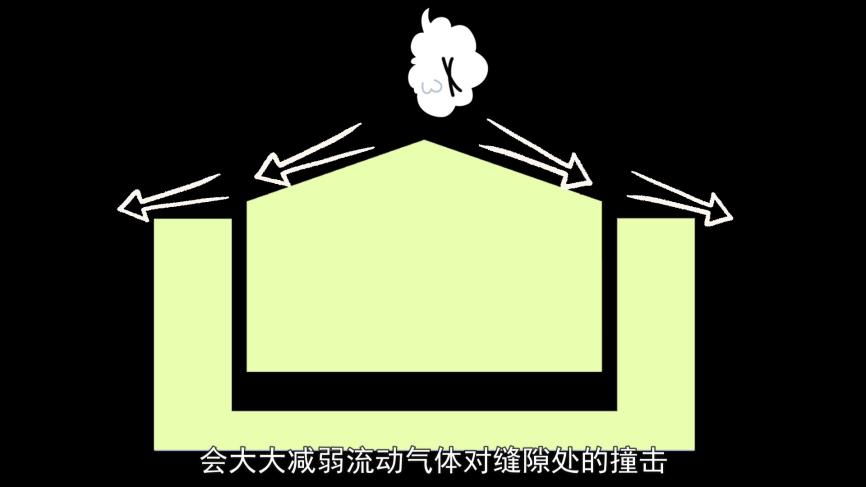
经过软件仿真分析，我们发现，当中间的木块被抬高后，其向上的压力几乎减少了十倍。

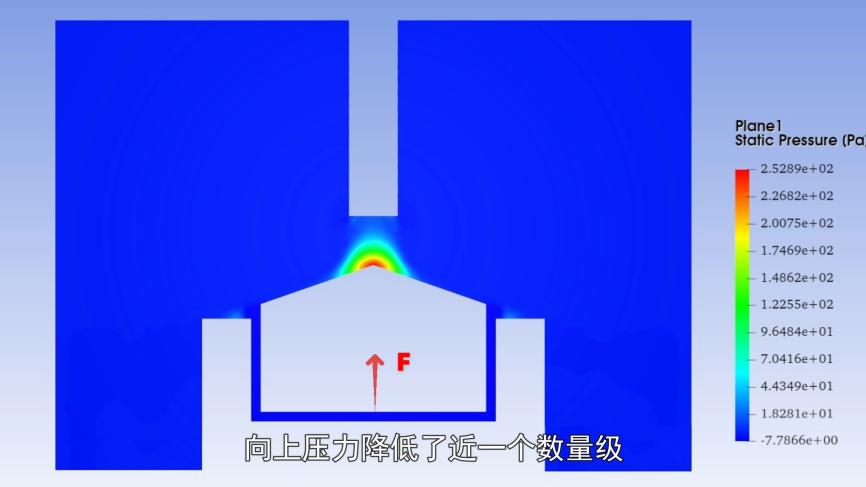
事实证明也确实更难吹出来，当然永远都可以大力出奇迹。

本期就到这啦，下期见~拜拜